Solve the following differential equation (x^2 y^2) dx – 2xy dy = 0 asked in Differential Equations by Amayra ( 314k points) differential equationsX 2 y xy 2 and g (x, y) = e −() xy 22, derive expressions for the partial derivatives ∂ ∂ ∂ ∂ f g f x xg and 4 Determine whether or not each of the following linear differential forms is an exact differential a dx xy dy 22xy b dx xy dy 22xy c 2 x 2 y dx x 3 dy d ln ydx x y dy 5 Evaluate each ofSolve the differential equation xydx(1x^2)dy=0 Grouping the terms of the differential equation Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side of the equality Simplify the expression \frac{1}{y}dy Simplify the expression x\frac{1}{1x^2}dx
Solve The Differential Equation Xy 2 X Dx X 2y Y Dy 0 Sarthaks Econnect Largest Online Education Community
Obtain the general solution (x^2+y^2)dx+(xy)dy=0
Obtain the general solution (x^2+y^2)dx+(xy)dy=0-Combine y 2 d x and x y 2 d to get 2 y 2 d x dx^ {3}2y^ {2}dx=0 d x 3 2 y 2 d x = 0 Combine all terms containing d Combine all terms containing d \left (x^ {3}2y^ {2}x\right)d=0 ( x 3 2 y 2 x) d = 0 The equation is in standard form The equation is in standard formIt is x minus two over access And we could also see clearly that X Y goes through zero when X is plus or minus square to to Um And then so this tells us that we have an oblique acetone at along the line X equals four, Y equals X We also have averted class and told the X equals zero You can take a derivative of the second derivative




7 X 2 Y 2 Dx X 2 2xy Dy 0 Ecuacion Diferencial Exacta Youtube
solve (x^2y)dy/dx2xy=0 → (2xy) dx (x^2y) dy=0 asked in CALCULUS by homeworkhelp Mentor derivativesThe equation (x^2 y^2 x )dx xydy =0 can be rewritten as dy/dx y/x = (x1)/y which is a Bernoulli equation The reduction to normal form is obtained taking y = V (x)^1/2 Then , dy/dx = (1/2) (V^1/2)V' and the equation becomes V' 2V/x =(x 2 y 2)dx 2xydy = 0 (x 2 y 2) dx = 2xydy `dy/dx = (x^2 y^2)/(2xy)`(i) The equation is a homogeneous equation Let y= vx, Differentiat ing wrt x, we get, `dy/dx=vx(dv)/dx` `dy/dx=(x^2y^2)/(2xy) " from "(i)` `vx(dv)/dx=(x^2(vx)^2)/(2x(vx))` `vx(dv)/dx=(1v^2)/(2v)` `x(dv)/dx=(1v^2)/(2v)v` `x(dv)/dx=(1v^22v^2)/(2v)` `x(dv)/dx=(1v^2)/(2v)`
2 Find an integrating factor and solve the following differential equation (x^2 y^2 x)dx xydy = 0;See the answer See the answer See the answer done loading Solve (x 2 y 2) dx xydy = 0 Best Answer This is the best answer based on feedback and ratings 100% (1 rating) Previous question Next question Get more help from Chegg Find the general solution of y2dx (x2xyy2)dy = 0 0 votes 128k views asked in Class XII Maths by nikita74 Expert (112k points) Find the general solution of y 2 dx (x 2 xyy 2 )dy = 0 differential equations
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byGiven The homogeneous differential equation is given as, (x2y2)dxxydy =0 ( x 2 y 2) d x x y d y = 0 To find the solution Rewrite the See full answer below




7 X 2 Y 2 Dx X 2 2xy Dy 0 Ecuacion Diferencial Exacta Youtube




Answered A Y2 Xy Dx X2 Xy Dy 0 Bartleby
Solve (x 2y 2)dx3xydy=0 =v In each of the Exercises 1 to 10, show that the given differential equation is homogeneous and solve each of them In each of the Exercises 1 to 10, show that the given differential equation is homogeneous and solve each of them Solve (x^2y^2x)dxxy dy =0 Get the answers you need, now! Ex 95, 6 Show that the given differential equation is homogeneous and solve each of them 𝑥 𝑑𝑦−𝑦 𝑑𝑥=√(𝑥^2𝑦^2 ) 𝑑𝑥 Step 1 Find 𝑑𝑦/𝑑𝑥 x dy − y dx = √(𝑥^2𝑦^2 ) dx x dy = √(𝑥^2𝑦^2 ) dx y dx x dy = (√(𝑥^2𝑦^2 )𝑦) dx 𝑑𝑦/𝑑𝑥 = (√(𝑥^2 𝑦^2 ) 𝑦)/𝑥 Step 2 Put 𝑑𝑦/𝑑𝑥 =




How To Find The Solution To The Equation Math X 2 Y 2 2x Dx 2ydy 0 Math That Satisfies Math Y 0 1 Math Quora



Solve The Following Differential Equation X 2 Y 2 Dx 2 Xydy 0given That Y 1 When X 1 Snapsolve
913 answers 1431K people helped (x^2 xy y^2)dx xydy =0 divide by x^2 (1y/x y^2/x^2) dx y/x dy = 0 Let y/x = v y=vx (1vv^2) dx v dy = 0 dy = (vdxxdv)Learn how to solve differential equations problems step by step online Solve the differential equation (x^23y^2)dx2xydy=0 We can identify that the differential equation \left(x^23y^2\right)dx2xy\cdot dy=0 is homogeneous, since it is written in the standard form M(x,y)dxN(x,y)dy=0, where M(x,y) and N(x,y) are the partial derivatives of a twovariableMultiply y and y to get y 2 \left (x^ {2}y^ {2}\right)dxxy^ {2}d=0 ( x 2 − y 2) d x − x y 2 d = 0 Use the distributive property to multiply x^ {2}y^ {2} by d Use the distributive property to multiply x 2 − y 2 by d \left (x^ {2}dy^ {2}d\right)xxy^ {2}d=0 ( x 2 d − y 2 d) x − x y 2 d = 0



Solve The Following Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 Sarthaks Econnect Largest Online Education Community




X 2 Y 2 Dx 2xy Dy 0 Youtube
y^2 = x^2(2lnx c) We can rewrite this Ordinary Differential Equation in differential form (x^2 y^2) \ dx xy \ dy = 0 A as follows \ \ \ \ dy/dx = (x^2 y^2)/(xy) dy/dx = x/y y/x B Leading to a suggestion of a substitution of the form u = y/x iff y = ux And differentiating wrt x whilst applying the product rule dy/dx = u x(du)/dx Substituting into the Transcript Ex 95, 12 For each of the differential equations in Exercises from 11 to 15 , find the particular solution satisfying the given condition 𝑥2𝑑𝑦 𝑥𝑦 𝑦2 𝑑𝑥=0;𝑦=1 When 𝑥=1 The differential equation can be written 𝑎s 𝑥2𝑑𝑦 = −(xy y2) dx 𝑑𝑦𝑑𝑥 = − 𝑥𝑦 𝑦2 𝑥2 Let F(xThey give you the integrating factor is x2, so multiply the whole equation by said factor to get (1y 2 /x 2)dx (12y/x )dy = 0 Now, check for exactness again, dM/dy = dN/dx (these should be partial derivatives) dM/dy = 2y/x 2 dN/dx = 2y/x 2 Therefore this equation is now exact, and solve it like you would any other exact equation



Solved Solve The Following Equations By The Method Of Separation Of Variables A Dy Dx 10x Y B 1 X 2 1 Y 2 Dx Xydy 0 C X 2 Dy Dx Course Hero



Find The General Solution Of Y 2dx X 2 Xy Y 2 Dy 0 Sarthaks Econnect Largest Online Education Community
Solution for Differential Equations Integrating Factors Solve the Equation (x2y2x)dxxydy=0For the differential equation `(x^2y^2)dx2xy dy=0`, which of the following are true (A) solution is `x^2y^2=cx` (B) `x^2y^2=cx` `x^2y^2=xc` (D) `ySolve the Differential Equation (x^2y^2)dxxydy=0 Find where Tap for more steps Differentiate with respect to Solve for Tap for more steps Move all terms containing variables to the left side of the equation Tap for more steps Subtract from both sides of the equation




In The Following Show That The Given Differential Equation Is Homogeneous And Solve Each Of Them 1 X 2 Xy Dy X 2 Y 2 Dx 2 Y X Yx



How To Solve Following By Variable Separation Method X 2 1 Y 2 1 Dx Xydy 0 Quora
The GS is y^2 = (A x^4)/(2x^2) Or, alternatively y = sqrt(A x^4)/(sqrt(2)x) We have (x^2 y^2) \ dx xy \ dy = 0 Which we can write in standard form as dy/dx = (x^2 y^2)/(xy) 1 Which is a nonseparable First Order Ordinary Differential Equation(X^2y^2x)dxxydy=0 Solve for general solution Mathematics Answer Comment 1 answer aksik 14 1 year ago 5 0 Check if the equation is exact, which happens for ODEs of the form if We have so the ODE is not quite exact, but we can find an integrating factor so that d x x d y 2 − y 2 d x x 2 = 0 d x d ( y 2 x) = 0 x y 2 x = C It seems to me that there is a sign mistake somewhere Share Follow this answer to receive notifications edited at 2301 answered at 2256 user



What Is The Solution To The Following Differential Equation X 2 Y 2 Dx 2xydy 0 Quora



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633
Solution for Solve the equation (x² – xy y² )dx – xydy = 0 %3D O (v x) el) = (v x) e(G) = c O (v x) = ce(÷)Solution for (x^2y^25)dx (yxy)dy=0 equation Simplifying (x 2 y 2 5) * dx 1 (y xy) * dy = 0 Reorder the terms (5 x 2 y 2) * dx 1 (y xy) * dy = 0 Reorder the terms for easier multiplication dx (5 x 2 y 2) 1 (y xy) * dy = 0 (5 * dx x 2 * dx y 2 * dx) 1 (y xy) * dy = 0 Reorder the terms (5dx dxy 2 dx 3) 1 (y xy) * dy = 0 (5dx dxy 2 dx 3) 1Dy / dx = f (y) Solve dy / dx = sin^2y Formation Of Differential Equations Form the differential equation of the family of curves represented c (y c)^2 = x^3 , where c is a parameter Find the differential equation that represents the family of all parabolas having




The General Solution Of The Differential Equation Y 2 X 3 Dx Xydy 0 X 0 Is Where C Is A Constant Of Integration



Differential Equations
Solve the following differential equation (x2 y2)dx 2xy dy = 0Solution for (x^2y^2)dx= (xy)dy equation Simplifying (x 2 1y 2) * dx = (xy) * dy Reorder the terms for easier multiplication dx (x 2 1y 2) = (xy) * dy (x 2 * dx 1y 2 * dx) = (xy) * dy Reorder the terms (1dxy 2 dx 3) = (xy) * dy (1dxy 2 dx 3) = (xy) * dy Multiply xy * dy 1dxy 2 dx 3 = dxy 2 Solving 1dxy 2 dx 3 = dxy 2 Solving for variable 'd'General solution of (x 2 y 2 ) dx 2xydy = 0 is y 2 x 2 = cx 2 x 2 y 2 = cx



Solved Bernoulli Equation Example B Solve X2 Y2 Dx Chegg Com



How To Solve The Homogeneous Differential Equation Xydy Dx Y 2 X 3 X 2 1 Quora
Show activity on this post solve the following differential equation (1) ( x 2 − 2 x 2 y 2) d x 2 x y d y = 0 d y d x = 2 x − x 2 − 2 y 2 2 x y dividing (1) throughout by y 2 we have, (2) ( x 2 y 2 2 − 2 x y 2) d x 2 ( x y) d y = 0 ordinarydifferentialequations ShareQuestion Solve (x2 y2 ) dx xydy = 0 This problem has been solved!The solution You have entered src 2 2 d x y (x) x*y (x) x* (y (x))*y (x) = 0 dx x 2 x y ( x) d d x y ( x) x y ( x) − y 2 ( x) = 0 x^2 x*y*y' x*y y^2 = 0 Detail solution Given the equation x 2 x y ( x) d d x y ( x) x y ( x) − y 2 ( x) = 0 Do replacement



Show That The Differential Equation X Y Dy Dx X 2y Is Homogeneous And Solve It Sarthaks Econnect Largest Online Education Community




X 2 Y 2 Dx 2xydy 0
The equation (x^2 y^2 x )dx xydy =0 can be rewritten as dy/dx y/x = (x1)/y which is a Bernoulli equation The reduction to normal form is obtained taking y = V (x)^1/2 Then , dy/dx =Question 2 Find an integrating factor and solve the following differential equation (x^2 y^2 x)dx xydy = 0The solution of the differential equation dy / dx = xy y / xy x is The solution of the differential equation x (dy / dx) 2y = x 2 is The solution of the equation (3 2 √2) x^28 (3 2 √2) 8x^2 = 6 are The Solution Of The Equation Sin X Cos X Power 1 Sin 2x 2 Pi X Pi Is The Solution Of Trigonometric Equation Cos 4 X Sin 4



Solve X 2 Y 2 Dx 2xy Dy 0 Sarthaks Econnect Largest Online Education Community




Y 2 X 2 Dy Dx Xy Dy Dx Youtube
Solution of the differential equation `(x^(2)2y^(2))dxxy dy=0,` when y (9)=0 isExample Solve the ODEs (x 2 y 2) dx2 xydy = 0 Here ∂ M ∂ y∂ N ∂ x N = 2 y 2 y2 xy =2 x (7) Then integrating factor is e R2 x dx = 1 x 2 Now multiplying by 1 x 2 (x 2 y 2) dx2 xy dy x 2 = 0 ⇒ d x 2y 2 x = 0 (8) which is exact and its solution is x 2y 2 = cx Ratikanta Behera Ordinary Differential Equations I September 1 Follow 0 Rishabh Mittal, Meritnation Expert added an answer, on 28/9/15 Rishabh Mittal answered this x x 2 y 2 y 2 dx xy dy = 0 x x 2 y 2 y 2 dx = xy dy dy dx = x x 2 y 2 y 2 xy = y 2 x x 2 y 2 xy = y 2 x 2 1 y 2 x 2 y x So , it is a homogeneous differential equation of degree zero Let y = vx dy dx = v x dv dx v




Differential Equation Dy Dx F X G X Can Be Solved By Separating Variable Dy G Y F X Dx The Equation Of The Curve To The Point 1 0 Which Satsifies The Differential Equation 1 Y 2 Dx Xydy 0 Is



Solved Consider The Differential Equation 3xy Y 2 Dx X 2 Xy Dy Course Hero
Assignment2 Homogeneous and Exact Differential Equations 1 Verify that the following differential equations are homogeneous Apply suitable substitution, solve these equations by separation variable method dy dy (i) (x2 − 2y 2 )dx xydy = 0 (ii) x2 y 0 − 3xy − 2y 2 = 0 (iii) y 2 x2 = xy dx dx y dy 3 dySolve the Differential Equation (x^2xyy^2)dxxydy=0 (x2 − xy y2)dx − xydy = 0 ( x 2 x y y 2) d x x yd y = 0 Nothing further can be done with this topic Please check the expression entered or try another topic (x2 − xyy2)dx−xydy = 0 ( x 2 x y y 2) d x x y d y = 0Soul soul Math Secondary School answered Solve (x^2y^2x)dxxy dy =0 2 See answers Advertisement Advertisement Brainly User Brainly User refer to the attachment Advertisement Advertisement




Engineering Mathematics Notes




Solve This 1 Dydx Y Y X X Y X 2 3xy Y2 Dx X2 Xy Dy 0 Maths Differential Equations Meritnation Com
Complete stepbystep answer A differential equation is an equation that relates one or more functions and their derivatives We are given the expression ( x 2 y 2) d x − 2 x y d y = 0 and we need to solve for this differential equation As a first step, we need to find Solve (y√(x^2y^2))dxxdy=0 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential Equations



Solve The Differential Equation Xy 2 X Dx X 2y Y Dy 0 Sarthaks Econnect Largest Online Education Community




Solve X 2 Yx 2 Dy Y 2 Xy 2 Dx 0




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube
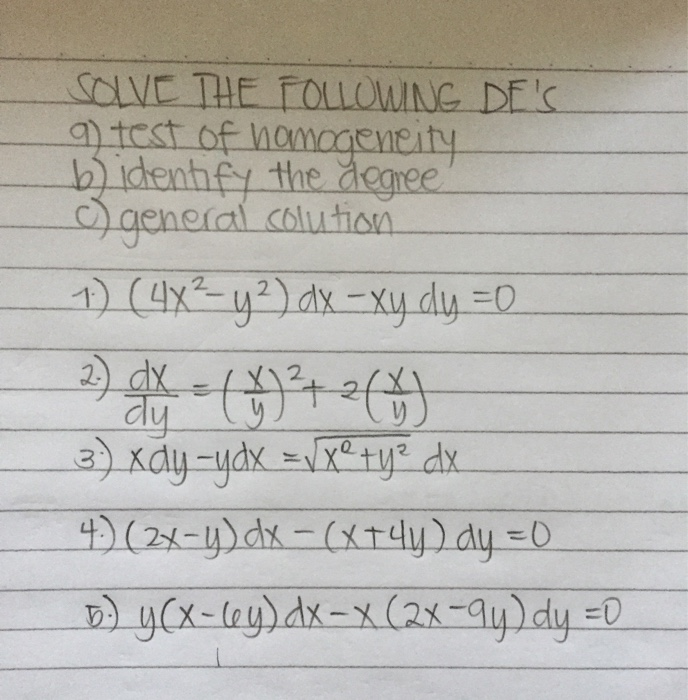



Solved Solve The Following De S G Test Of Homogeneity B Chegg Com



1




Engineering Mathematics Notes



Solved X2 Y2 X Dx Xy Dy 0 14 Solve The Differential Chegg Com




The General Solution Of The Differential Equation Y 2 X 3 Dx Xydy 0 X 0 Is Brainiak




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
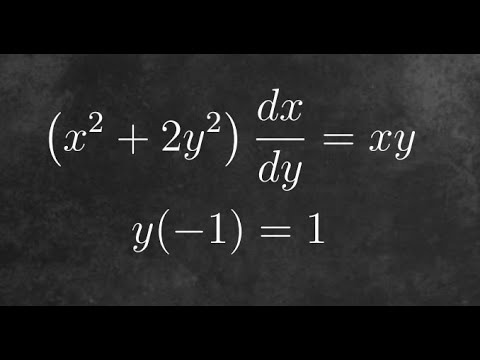



X 2 2y 2 Dx Dy Xy Homogeneous Substitution Youtube




Obtain The General Solution Of The Following Different Itprospt




Solve The Following Differential Equation 12 Sqrt 1 X 2 Y 2 X 2 Y 2 Dx Xydy 0 Snapsolve



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community
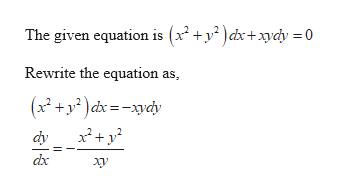



Answered Solve The Homogeneous Equations X2 Bartleby




Solve The Differential Equation 1 X 2 Y 2 X 2y 2 Xy Dydx 0



What Is The Integrating Factor Of 2x Y X Dx Xydy 0 Quora



Solved Subject Test For Exactness And Solve If Exact 1 Y 2 Xy 2 Dx X 2 Y Y 2xy Dy 0 2 Xy 2 Y X Dx X Xy 1 Dy 0 3 Course Hero




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Differential Equations Homogeneous Differential Equations Part 2 Discussion Recorded Via Zoom Youtube
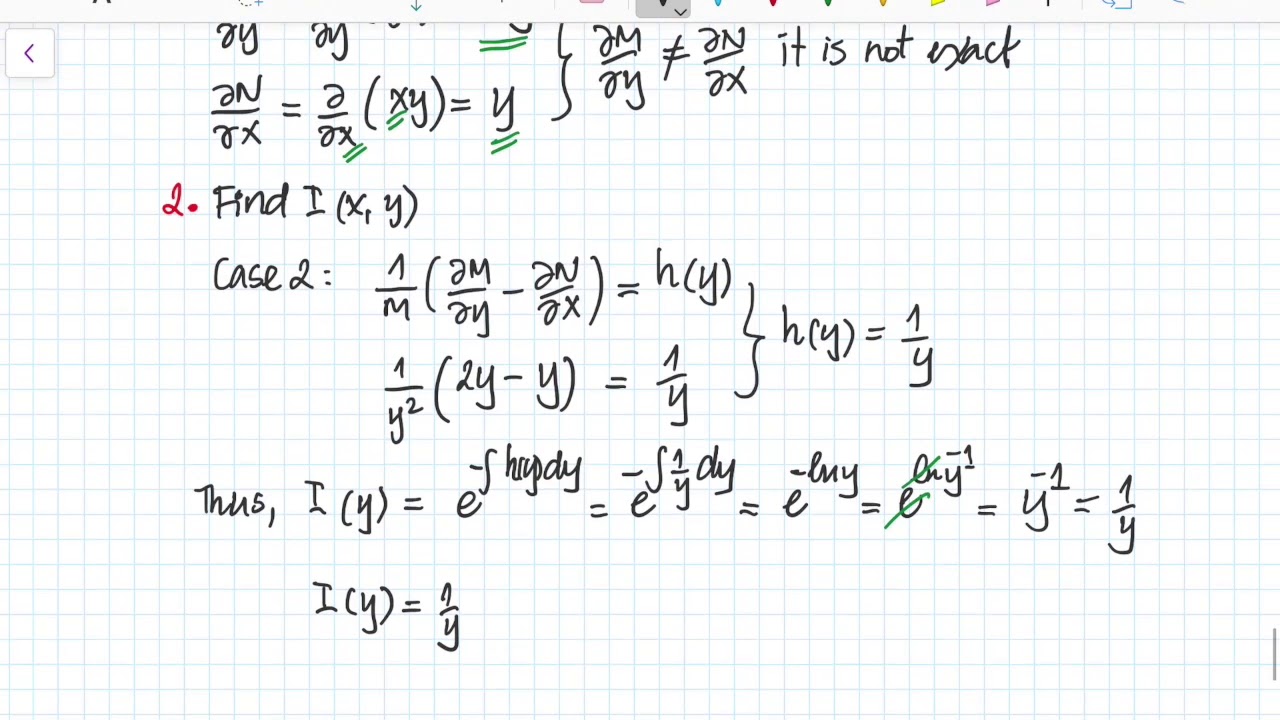



Y 2dx Xy Dy 0 Youtube




Solve The Following Differential Equation 3xy Y2 Dx X2 Xy Dy 0 For X 1 Y 1 Brainly In



How To Solve The Differential Equation Xy Dx X 2 2y 2 Dy 0 Quora




The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx X Xy X 2y 2 Dy 0 Is Given Youtube




Show That The Given Differential Equation Is Homogeneous And Solve Each Of Them X2 Xy Dy X2 Y2 Dx Mathematics Shaalaa Com



Solved Questions Solve X Y Dx Xy Dy 0 2 Solve Dy Chegg Com




Solve X2 Xy Dy X2 Y2 Dx Brainly In




If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5
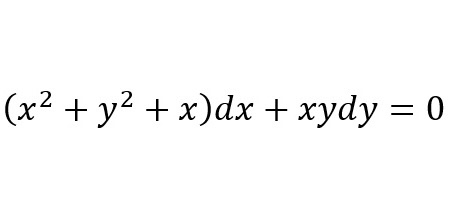



Solved X2 Y2 X Dx Xydy 0 Chegg Com
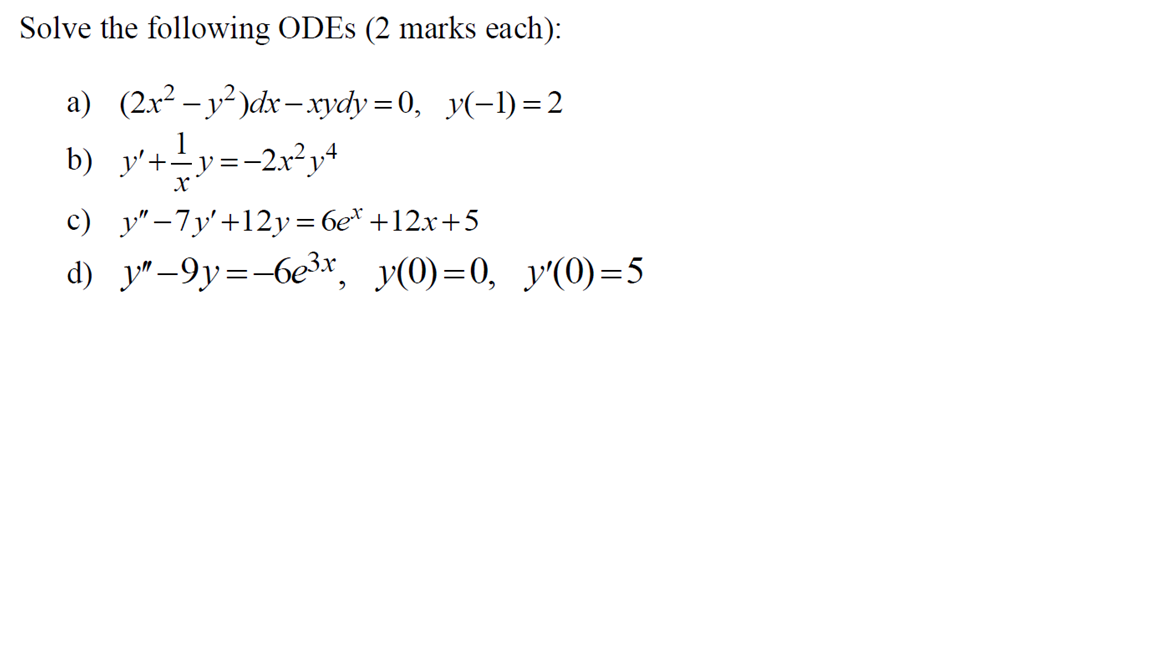



Solved Solve The Following Odes A 2x 2 Y 2 Dx Xydy 0 Chegg Com




Solved 4 Ey 5 X Dx Xydy Dx 5 Dy Y2 Y 0 X2 X B Chegg Com




Solve The Differential Equation X 2 Y 2 Dx 2xydy 0




Find The G S Of The De 3xy Y2 Dx X X Y Dy 0 Homeworklib




Solved Exercises Obtain Family Of Solutions 1 X 2y Dx 2x Y Dy 0 2 2 2x2 Y2 Dx Xydy 0 3 Xydx X2 3y2 Dy 0 4 Xy




Solved The Equation X 2 Y 2 Dx Xy Dy 0 Is Not Exact Chegg Com



Solved Solving Exact First Oder Differential Equations Course Hero




Express X Sqrt X 2 Y 2 Y 2 Dx Xy Dy 0 In The Form Dy Dx F Y X



Solved Solving Exact And Non Exact Differential Equation Chegg Com



How To Solve This Differential Equation Y Xy 2 Dx X X 2 Y 2 Dy 0 Quora



How To Solve This With Separable Variables Y 2 X 2 Dx Xydy 0 Quora




Solved Solve The Given Differential Equation A X 2 Chegg Com



What Is The Solution For Math Sqrt 1 X 2 Sqrt 1 Y 2 Dx Xy Dy 0 Math Quora



What Is The Solution To X 2 Y 2 X Dx Xydy Quora




Solved Solve Each Differential Equation X Dy Y 2 Dx 0 Chegg Com



How Would You Solve The Equation X Y Dx X Y Dy 0 Quora



3x Y Y 2 Dx X 2 X Y Dy 0 Youtube




Solve X 2 Y 2 X Dx Xy Dy 0 Brainly In




Ex 9 5 12 Find Particular Solution X2 Dy Xy Y2 Dx 0
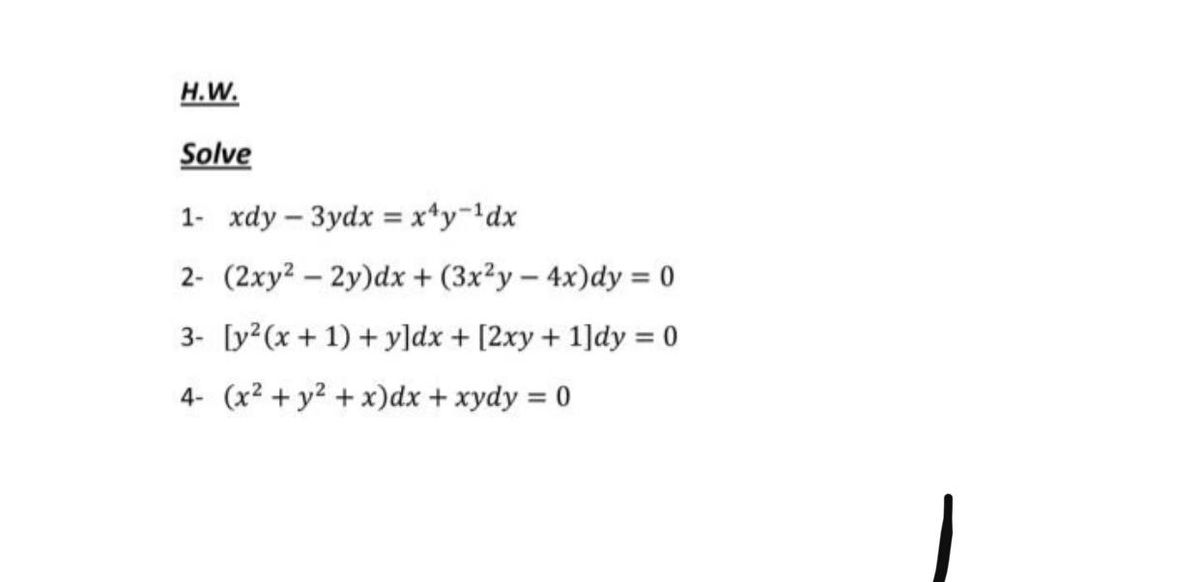



Answered N W Solve 1 Xdy 3ydx X Y Dx 2 Bartleby




Solve Y 2dx X 2 Xy Dy 0



What Is The Solution To 3 3x 2 Y 2 Dx 2xydy 0 Quora




Solved Solve Each Differential Equation Xdy Y 2 Dx 0 Chegg Com



X 2 Y 2 Dx Xydy 0 Novocom Top



How To Solve The Following Differential Equation X2 Y2 1 Dx 2xydy 0 Quora



Solved Bernoulli S Equation 6y 2 Dx X 2x 3 Y Dy 0 Chegg Com



Solve Y 2dx X 2 Xy Y 2 Dy 0 Youtube



Solved Differential Equations X 2 Y 2 Dx Xy Dy Chegg Com




Ordinary Differential Equations Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



How To Show That The Differential Equation X Y Dx 2xydy 0 Is Exact And Hence Solved Quora




Solve D Yd X X 2 1 Y 2 1 X Y 0
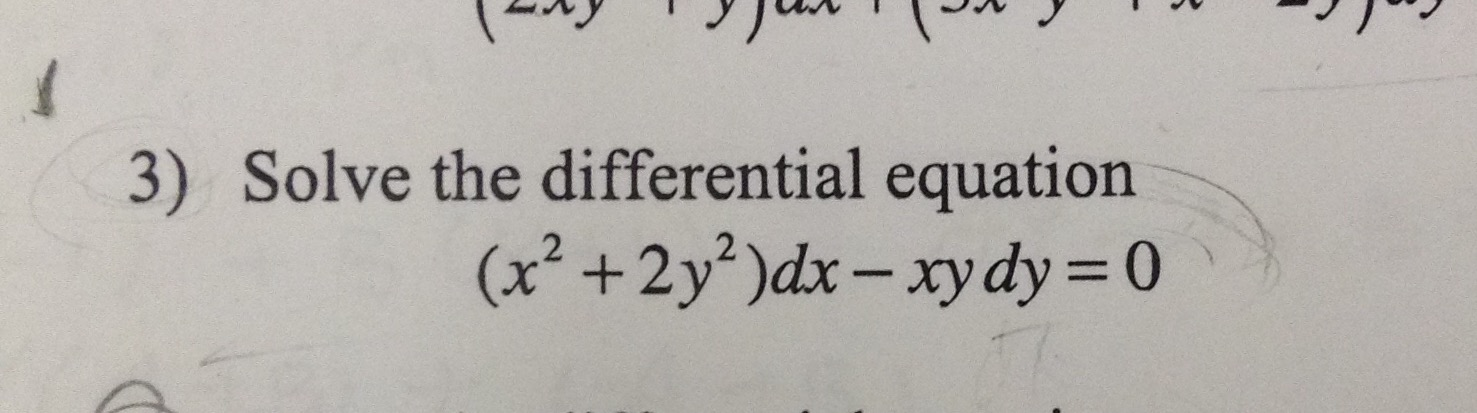



Solved 3 Solve The Differential Equation X 2 2y 2 Dx Xy Chegg Com
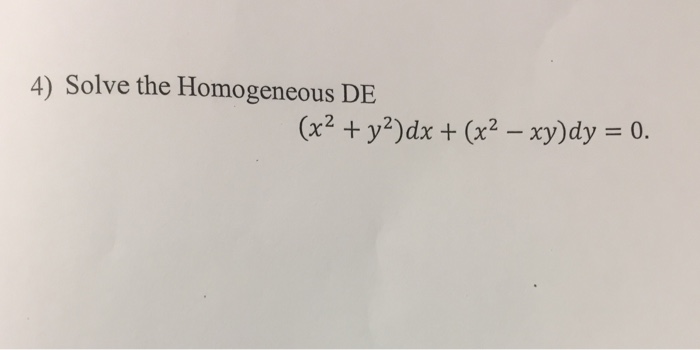



Solved Solve The Homogeneous De X 2 Y 2 Dx X 2 Xy Dy Chegg Com
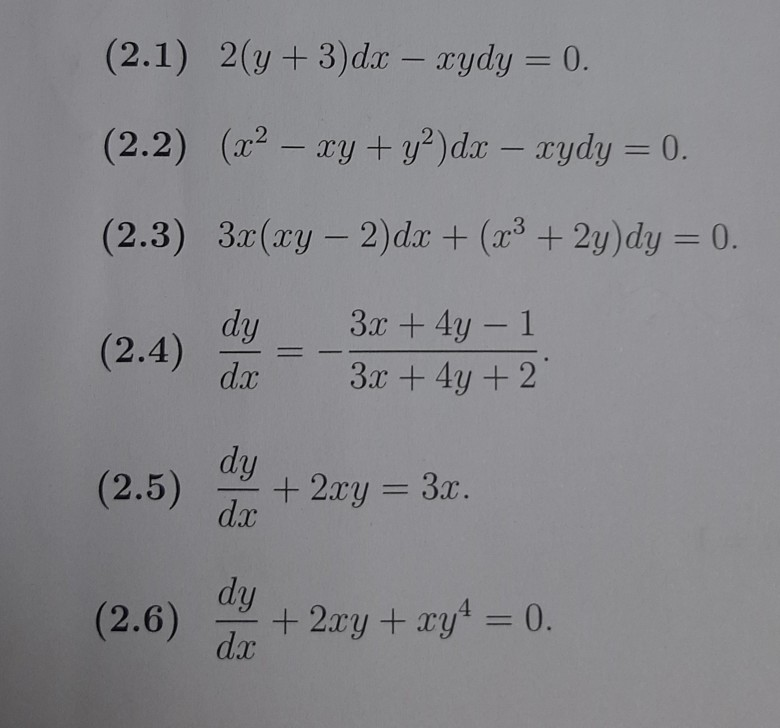



Solved 2 1 2 Y 3 Dx Xydy 0 2 2 X2 Xy Y Dx Chegg Com




Ipe Material Notes




Solved 1 Show That 2x2 Y2 Dx Xy Dy 0 Is A Chegg Com
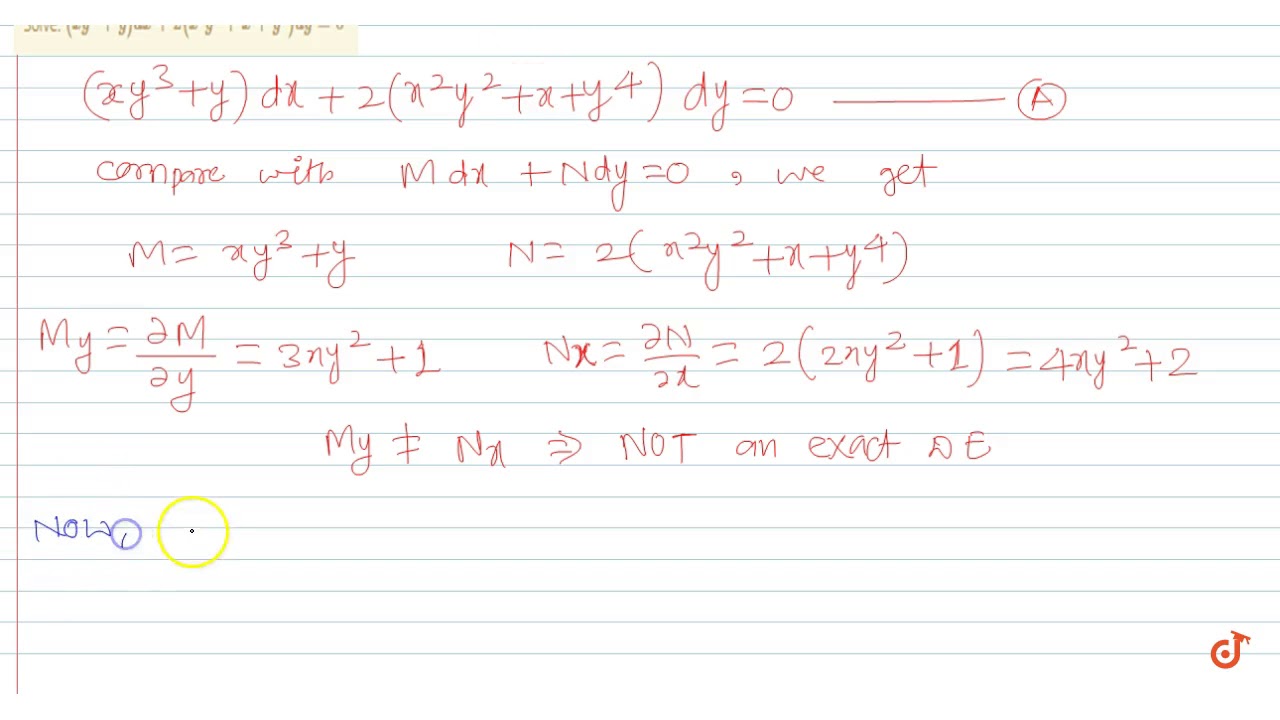



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube



The General Solution Of The Differential Equation Y 2 X 3 Dx Xydy 0 X 0 Is Where C Is A Constant Of Integration Sarthaks Econnect Largest Online Education Community
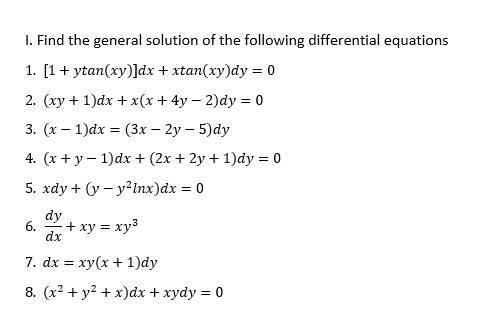



Solved I Find The General Solution Of The Following Chegg Com




First Order Differential Equations Ppt Download



What Is The Solution Of The Homogeneous Problem Xydx X 2 Y 2 Dy 0 Quora




Solved Find An Integrating Factor And Solve The Following Chegg Com




Ex 9 5 11 Find Particular Solution X Y Dy X Y Dx 0




Ans X C E P U 4 Une Dx 14 Solve X Y Dx 2xy Dy 0 Ans Y X Cx 15 Solve Xy Dy Idy 2 12




Linear Algebra Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




Solve X Y X Dx Xydy 0 Brainly In



1



What Is The Value Of 4y 3x Dy Y 2x Dx 0 Quora




Solved Question 2 Solve The Following Differential Chegg Com


